⏭playDataAlgo 동적계획법

⏭동적계획법(Dynamic Programming)

---

💢동적계획법이란??

• 하나의 큰 문제를 여러 개의 공통되는 작은 문제로 나누어서 작은 문제의 정답들을 결합하여 알고리즘을 푸는 과정(규칙을 찾아가는 과정)

---

❗점화식

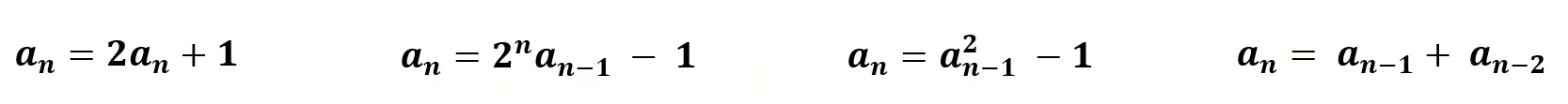
<위>

위 그림과 같이 수열에서 n번째 항을 이전에 나온 항들로 나타낸 공식

아래 예시로 여러가지 점화식 구현도 가능하다.

✅ex1)

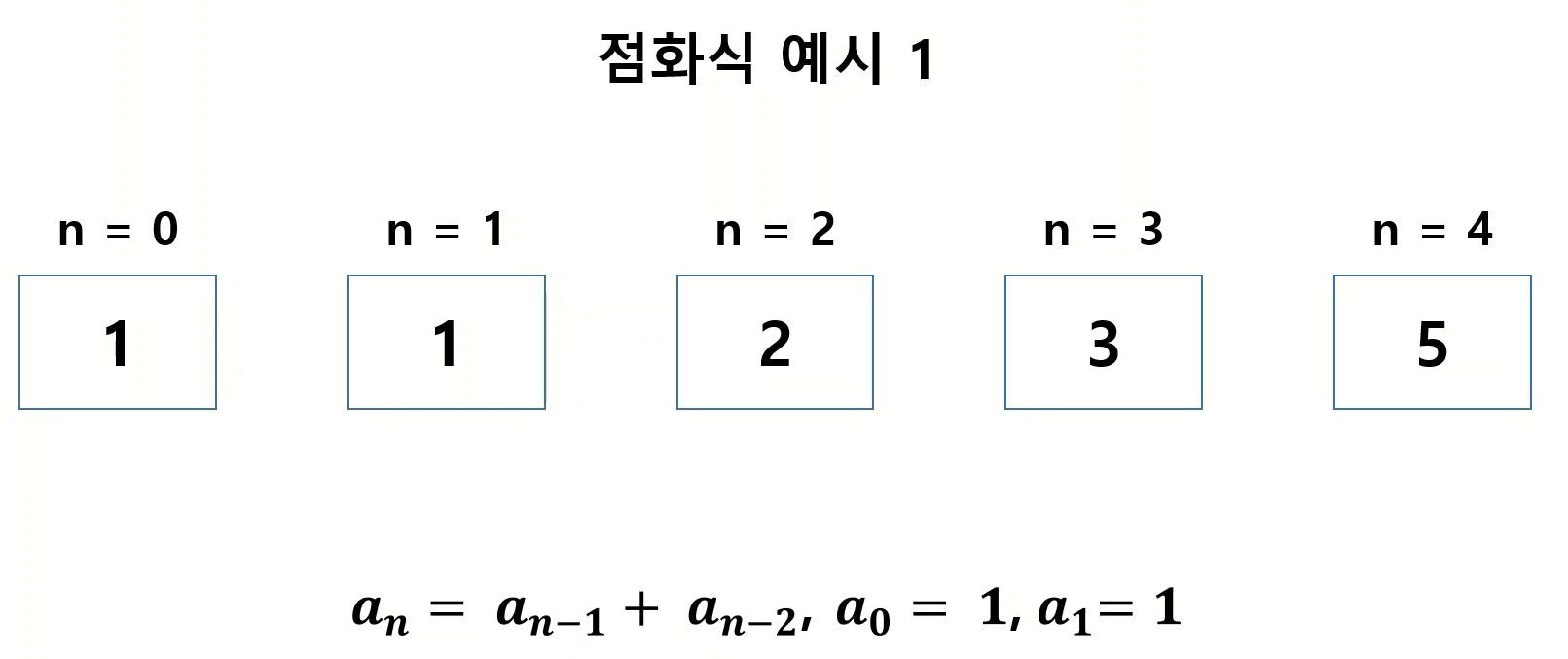
✅ex2)

---

❗동적계획법 접근방법

동적계획법에는 작은 것부터 구현하여 결합식히는 형식의 Bottom up과 큰것들을 쪼개는 형식의 Top Down방식으로 구현한다.

---

❗동적계획법 활용

✅Bottom up

        for i in range(2, n+1):
            fibList.aoppend(fibList[i-2] + fibList[i-1])    
            return fibList[-1]

✅Top Down

        if n ==0 or n ==1:
            return 1 
        else: 
            return (fib(n-1) + fib(n-2))

위에 사진을 보면 알 수 있듯이 Top down은 많은양의 계산이 필요하고 계산 중복, 이를 해결하기 위한 것이 메모이제이션이다.

---

❗메모이제이션

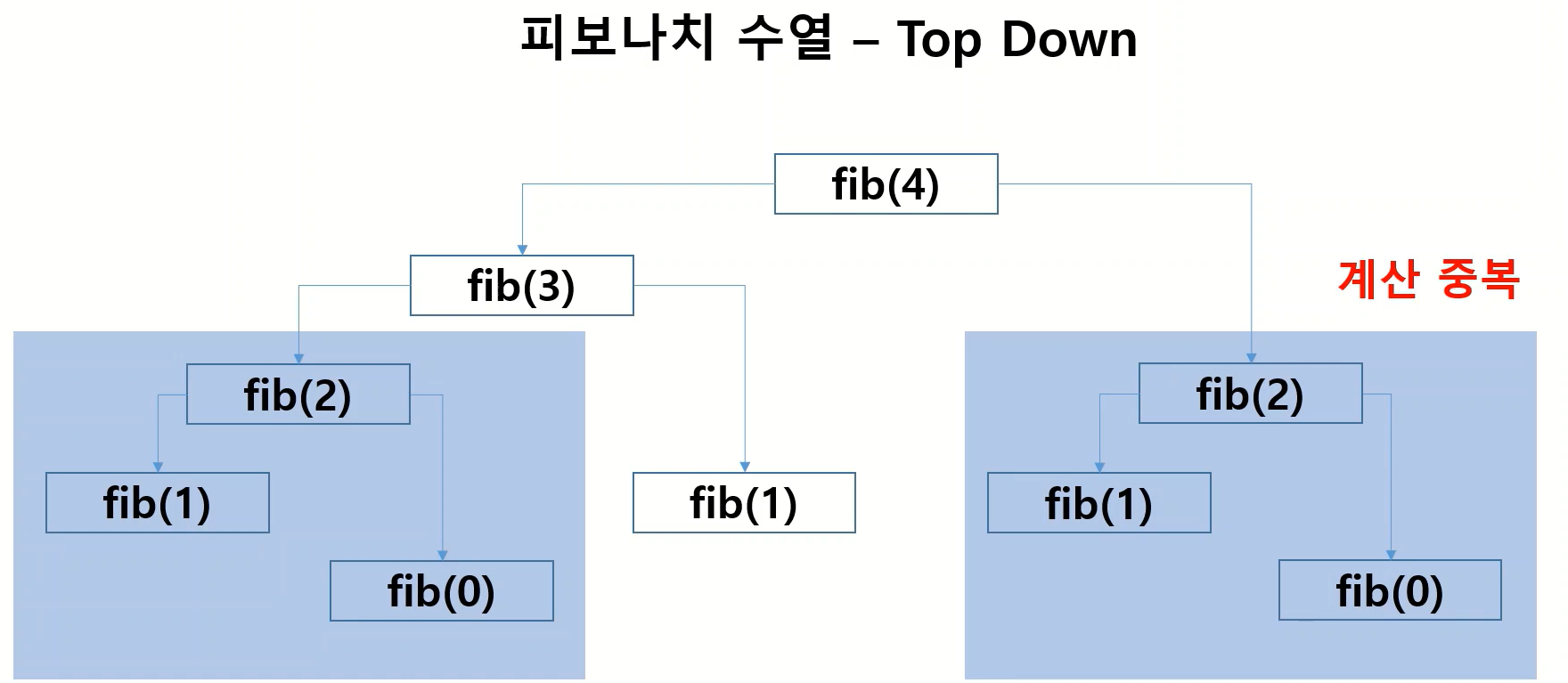
중복을 최소화하기 위해 배열 혹은 해시를 활용하는 것이 핵심

memo = {0:1, 1:1}

def fib(n):
    if n in memo:
        return memo[n] #메모안에 값이 있다면 출력
    else:
        result = fib(n-1) + fib(n-2)
        memo[n] = result
        return result

---

동적계획법 예시

이웃하지 않은 숫자들의 합의 최대값은?

data = [3, 4, 5 ,6, 1, 2, 5]

def solution(data):
    if len(data) == 1:
        return data[0]
    result = [data[0], max(data[0], data[1])]
    for i in range(2, len(data)):
        result.append(max(result[i-1], result[i-2] + data[i])
        return result[-1]

1:3

2: max(3, 4)->5

3:max(3+5, 4) ->8

4:max(8, 6+4) -> 10

5:max(10, 8+1) -> 10

6:max(10, 10+2) -> 12

7:max(12, 10+5) -> 15

위와 같은 형식의 포멧으로 과정들을 숫자로 하나씩 나열해보면 이웃하지 않은 수들의 최댓값을 추출할 수 있다.